1. 题目描述
- 来源:力扣(LeetCode)
- 链接:https://leetcode-cn.com/problems/next-permutation
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。
例如,
arr = [1,2,3],以下这些都可以视作arr的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1]。 整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地,如果数组的所有排列根据其字典顺序从小到大排列在一个容器中,那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列,那么这个数组必须重排为字典序最小的排列(即,其元素按升序排列)。- 例如,
arr = [1,2,3]的下一个排列是[1,3,2]。 - 类似地,
arr = [2,3,1]的下一个排列是[3,1,2]。 - 而
arr = [3,2,1]的下一个排列是[1,2,3],因为[3,2,1]不存在一个字典序更大的排列。
给你一个整数数组 nums ,找出 nums 的下一个排列。
必须 原地 修改,只允许使用额外常数空间。
示例 1:
1
2
输入:nums = [1,2,3]
输出:[1,3,2]
示例 2:
1
2
输入:nums = [3,2,1]
输出:[1,2,3]
示例 3:
1
2
输入:nums = [1,1,5]
输出:[1,5,1]
提示:
1 <= nums.length <= 1000 <= nums[i] <= 100
2. 题解
以arr=[1,2,3]为例,其字典序排列如下:
[1,2,3], [1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]
可以发现,一般情况下,下一个排列所组成的数值都要比当前排列要大(如[1,3,2] > [1,2,3]);如果当前排列是最后一个排列([3,2,1]),则下一个排列(即第一个排列,[1,2,3])可视为当前排列的反序输出。
因此,此题的目的可以描述为:针对一个当前序列arr=[x0,x1,x2,x3,...,xn],一般情况下,需要找到一个新的序列arr'=[y0,y1,y2,y3,...,yn],同时需要满足arr'>arr,且arr'需要尽可能的小。
算法流程如下(废话连篇版):给定当前序列arr=[x0,x1,x2,x3,...,xn],以[1,3,5,4,2]为例
- 从右到左遍历序列
arr,找到第一个满足x(i) < x(i+1)的位置i。针对示例,3<5满足要求,因此我们找到了位置i=1,即x1=3。这样做的目的在于:对于xi右边的子序列[x(i+1),...,xn],左数均比右数大,因此这个子序列是没有变大的空间的,它的下一个排列只能是[xn,...,x(i+1)]。但是找到的数字x(i),则可以用其右边的某一个比它大的数与之交换,整个序列就变大了。 - 第1步中,我们找到了一个较小的数
x(i),现在则需要从其右边的子序列[x(i+1),...,xn]中找到最接近x(i)且大于x(i)的数x(j),同样通过从右到左遍历序列arr[i:]=[x(i+1),...,xn],找到第一个满足x(j) > x(i)的位置j,并进行数据x(i)和x(j)的交换。针对示例,4>3满足要求,因此找到了位置j=3,即x3=4。这样做的目的在于:要获取下一个序列,因此需要大于当前序列,但又不能太大,从第1步可知,arr[i:]=[x(i+1),...,xn]序列是降序排列的,因此从右往左遍历找到的第一个大于x(i)的值即满足要求。 - 现在得到了新的序列
[x0,x1,...,x(j),x(i+1)..,x(j-1),x(i),x(j+1),...,xn],我们可以确定这个序列肯定比当前序列arr=[x0,x1,...,x(i),x(i+1)..,x(j-1),x(j),x(j+1),...,xn]要大(因为x(j)>x(i)),但会不会大过头了?因此我们还需要判断子序列[x(i+1)..,x(j-1),x(i),x(j+1),...,xn]是不是足够小(把这个子序列变为升序排列就足够小了!)。从第1第2步我们可以知道,初始序列的子序列[x(i+1)..,x(j-1),x(i),x(j+1),...,xn]是降序排列的,显然不够小,那交换之后的子序列x(i+1)..,x(j-1),x(i),x(j+1),...,xn]呢?也是降序排列的,所以我们只需要把这部分子序列反转就可以得到最终的结果了。
算法流程如下(图示版):以[1,3,5,4,2]为例
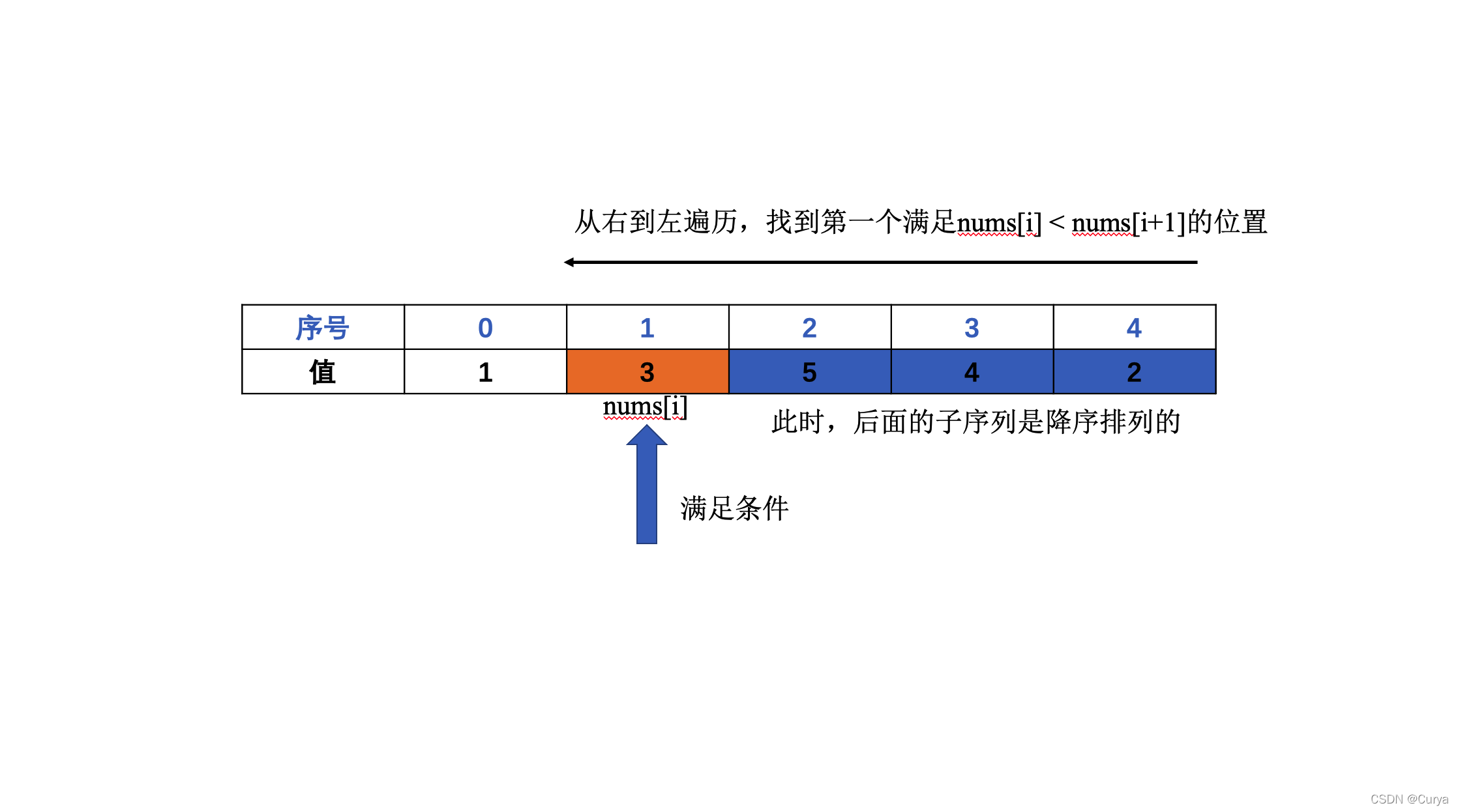
步骤1:从右到左遍历,找到第一个找到第一个满足
nums[i] < nums[i+1]的位置,即nums[1]=3;![在这里插入图片描述]()
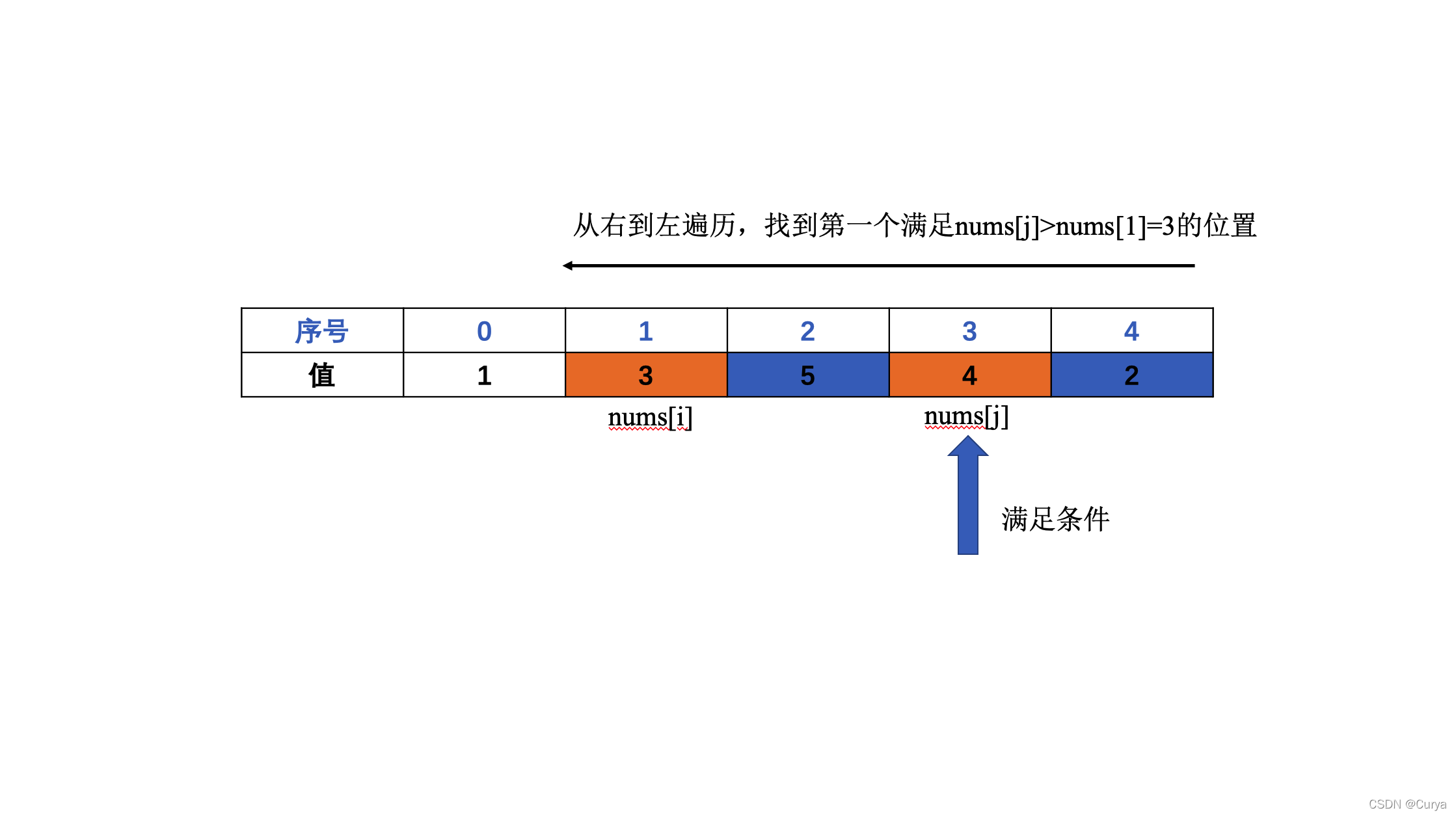
- 步骤2:从子序列中,从右到左遍历,找到第一个满足
nums[j]>nums[1]=3的位置,即nums[3]=4![在这里插入图片描述]()
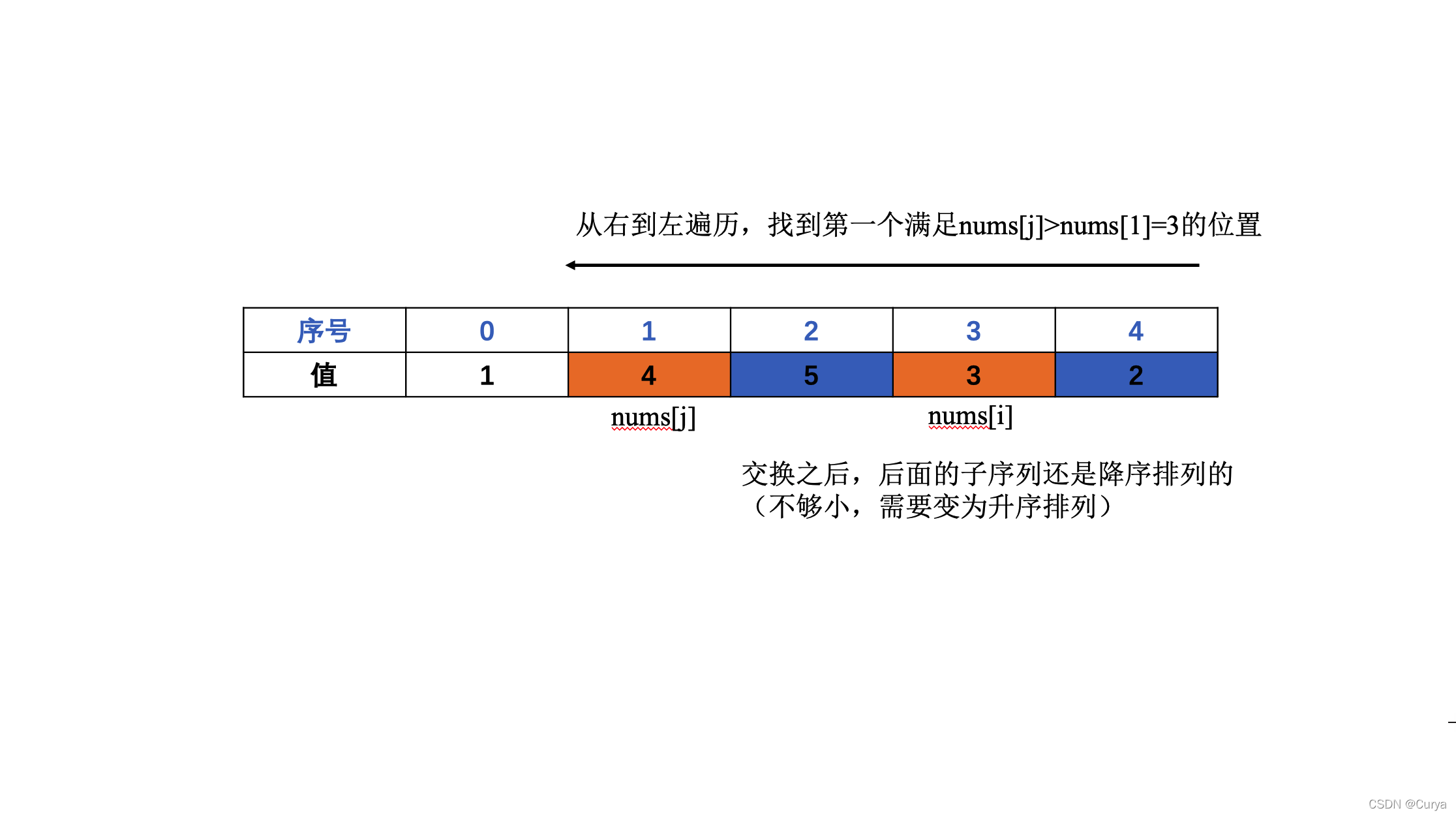
![在这里插入图片描述]()
- 步骤3: 将后面的子序列反转,变为升序排列,得到最终结果
[1,4,2,3,5]![在这里插入图片描述]()
3. 代码实现
Python实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution:
def nextPermutation(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
left = len(nums) - 1 - 1
while left >= 0 and nums[left] >= nums[left+1]:
left -= 1
if left >= 0:
right = len(nums) - 1
# 找到从右往左第一个比left值大的数
while right >= left and nums[right] <= nums[left]:
right -= 1
# 交换
nums[left], nums[right] = nums[right], nums[left]
# 反转left后的数值
left, right = left + 1, len(nums) - 1
while left < right:
nums[left], nums[right] = nums[right], nums[left]
left += 1
right -= 1
C++实现
我还没写