LeetCode97-交错字符串

1. 题目描述

• 来源：力扣（LeetCode）
• 链接：https://leetcode.cn/problems/interleaving-string
  著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

给定三个字符串 s1、s2、s3，请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的。

两个字符串 s 和 t 交错 的定义与过程如下，其中每个字符串都会被分割成若干 非空 子字符串：

• $s = s_1 + s_2 + … + s_n$
• $t = t_1 + t_2 + … + t_m$
• $ |n - m| <= 1 $
• 交错 是 $s_1 + t_1 + s_2 + t_2 + s_3 + t_3 + …$ 或者 $t_1 + s_1 + t_2 + s_2 + t_3 + s_3 + …$

注意：a + b 意味着字符串 a 和 b 连接。

示例 1：

输入：s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
输出：true

示例 2：

输入：s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc"
输出：false

示例 3：

输入：s1 = "", s2 = "", s3 = ""
输出：true

提示：

• 0 <= s1.length, s2.length <= 100
• 0 <= s3.length <= 200
• s1、s2、和 s3 都由小写英文字母组成

进阶：您能否仅使用 O(s2.length) 额外的内存空间来解决它?

2. 题解

动态规划！！！动态规划！！！（其实第一反应是用递归求解，但是超时了）

如果s3 可以由 s1 和 s2 交错 组成，那么用一个二维数组DP可以比较直观的表示出交错方式。以示例 1为例，s1 = "aabcc"，s2 = "dbbca"，s3 = "aadbbcbcac"，交错方式可表示如下:

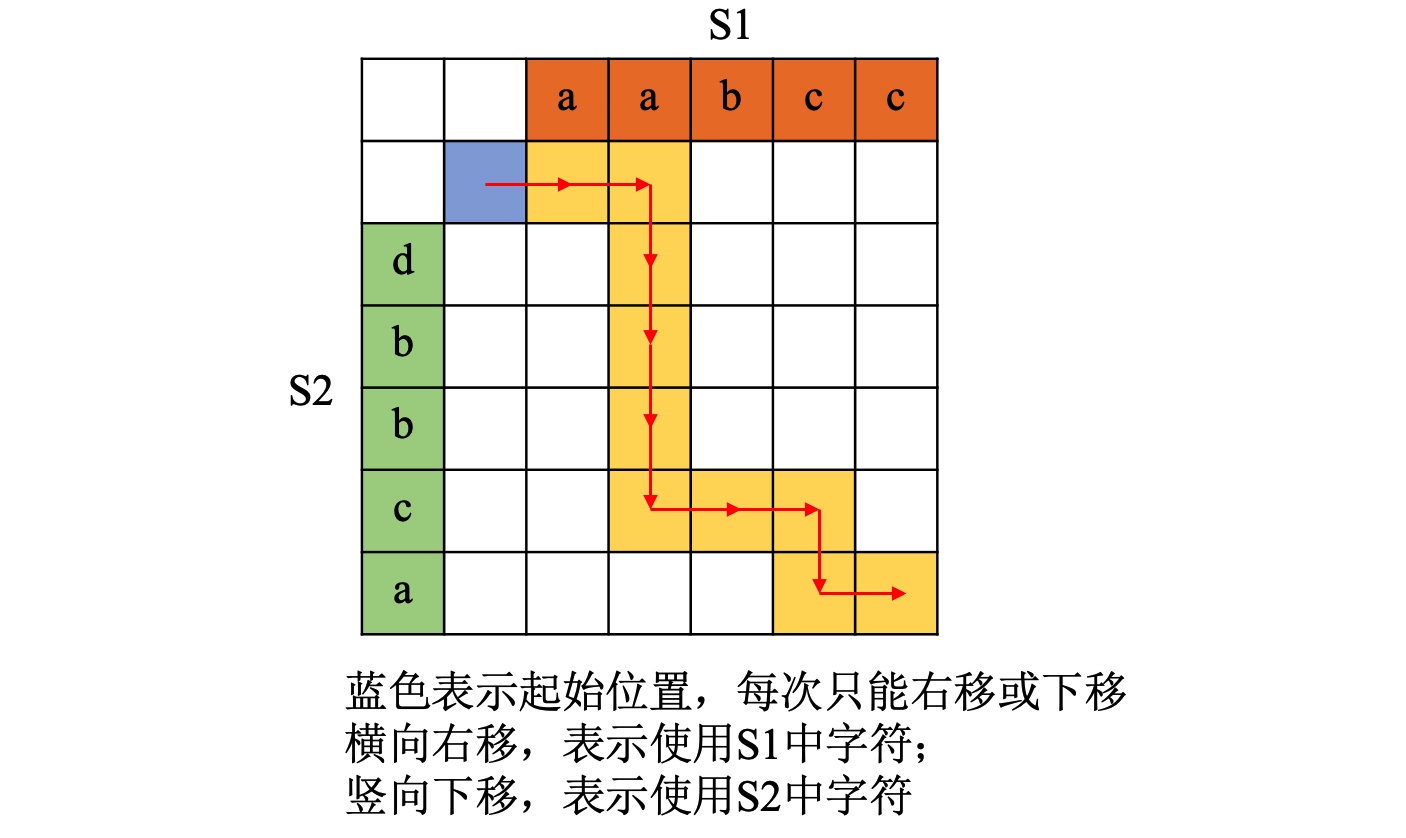
如果路径最终能够到达二维数组右下角最后一个位置DP[-1][-1]，则说明输入有解，返回True，否则返回False。但是如何判断路径能够到达右下角位置呢？可以对数组DP中数据进行编号（初始化为-1），起始位置为0，当DP更新完成之后，判断DP[-1][-1]的值是否等于S3.length即可，如图。

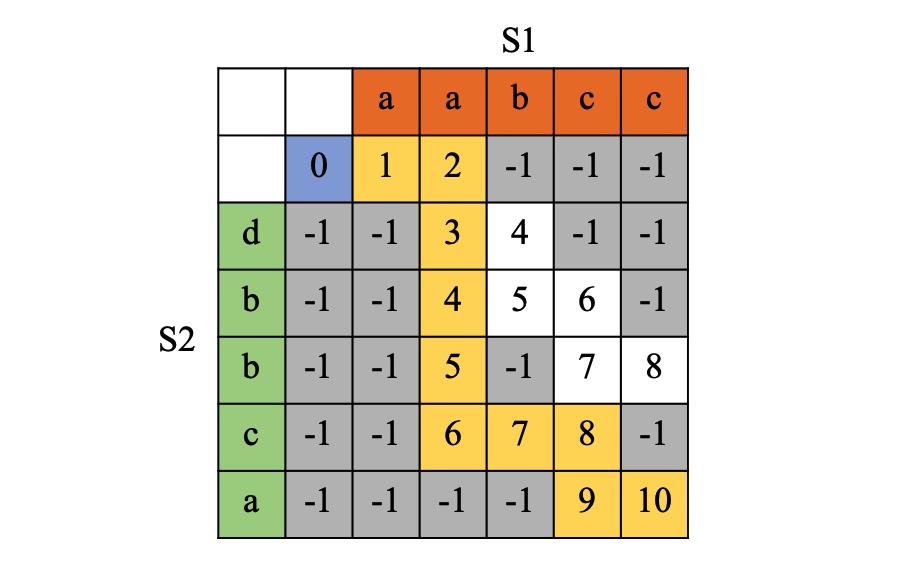
其中，灰色为初始化的数值，蓝色为起始位置，黄色为真正有效的交错路径，白底的则是不满足要求的可部分交错的一些位置。

接下来的问题就是，如何对二维数组DP进行更新，算法流程如下：

1. 创建二维数组DP，大小为(s2.length+1)*(s1.length+1)，所有数值初始化为-1；
2. DP[0][0]置为0，表示起始位置；
3. 遍历DP数组每一个元素，因为在交错路径中，只能 向右 / 向下 移动（向右表示使用S1中一个字符，向下表示使用S2中一个字符），所以对于任意位置DP[i][j]，我们只需要考虑其 左 / 上 位置的数值left / up（如果位置越界，则取其数值为-1即可）是否满足一定要求，然后对DP[i][j]进行数值更新即可：
   • 如果数值left >= 0，说明当前交错路径可以到达DP[i][j-1]（即S3[left-1]可以与S1或者S2中的一个字符匹配）。这时我们需要判断路径是否可以右移到DP[i][j]，即判断S3[left]是否与S1[j-1]匹配。如果匹配，则令DP[i][j] = left + 1。
   • 如果数值up >= 0，说明当前交错路径可以到达DP[i-1][j]（即S3[up-1]可以与S1或者S2中的一个字符匹配）。这时我们需要判断路径是否可以下移到DP[i][j]，即判断S3[up]是否与S2[i-1]匹配。如果匹配，则令DP[i][j] = up + 1。
4. 整个数组DP更新完成之后，判断DP[-1][-1]是否等于S3.lenght。

进阶 要求则需要创建一维数组DP，遍历时动态复用。

3. 代码实现

Python实现

class Solution:
    def isInterleave(self, s1: str, s2: str, s3: str) -> bool:
        # 一些可以直接返回结果的特殊情况
        if len(s1) + len(s2) != len(s3):
            return False
        if len(s1) + len(s2) == len(s3) == 0:
            return True
        
        # 一般情况
        n1 = len(s1)
        n2 = len(s2)
        n3 = len(s3)
        DP = [[-1] * (n1 + 1) for _ in range(n2 + 1)] 
        DP[0][0] = 0
        for i in range(n2 + 1):
            for j in range(n1 + 1):
                if i == 0 and j == 0:
                    continue
                left = DP[i][j-1] if j - 1 >= 0 else -1
                up   = DP[i-1][j] if i - 1 >= 0 else -1
                if left >= 0 and s3[left] == s1[j-1]:
                    DP[i][j] = left + 1
                if up >= 0 and s3[up] == s2[i-1]:
                    DP[i][j] = up + 1
                    
        return DP[-1][-1] == n3