Home 四种Normalization的计算差异
Post
Cancel

四种Normalization的计算差异

Posted 2022-07-07 Updated 2023-05-15 10 min read

Refs: 深度学习中的Normalization方法

将输入维度记为$[N, C, H, W]$，在计算操作上，不同Normalization的主要区别在于：

  • Batch Normalization：在Batch Size方向上，对NHW做归一化，对batch size大小比较敏感；
  • Layer Normalization：在Channel方向上，对CHW归一化；
  • Instance Normalization：在图像像素上，对HW做归一化，多用于风格化迁移；
  • Group Normalization：将Channel分组–>[B, g, C//g, H, W]，然后再对后三个维度做归一化（和InstanceNorm和LayerNorm都相似之处）；

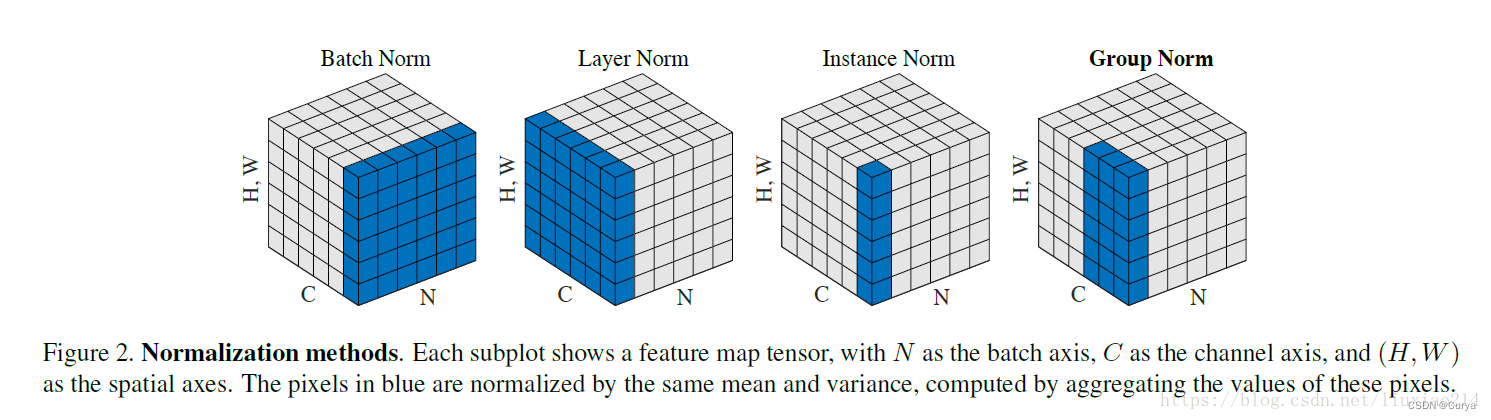
不同Normalization图示

以下针对Pytorch中不同Normalizaiotn计算示例，均忽略可学习的仿射变换参数$\gamma$和$\beta$。

1. BatchNorm2d

API: CLASS torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True, device=None, dtype=None)

\[y=\frac{x-\text{E}[x]}{\sqrt{\text{Var}[x] + \epsilon}} * \gamma + \beta\]
  • 输入: [N, C, H, W]
  • 输出: [N, C, H, W]

在NHW上计算均值和方差，代码示例如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

# input data
N, C, H, W = 3, 5, 2, 2
x = torch.rand(N, C, H, W)  # [N, C, H, W]

# nn.BatchNorm2d 计算
bn_layer = torch.nn.BatchNorm2d(C, eps=0., affine=False, track_running_stats=False)
x_out_1 = bn_layer(x)  # [N, C, H, W]

# 按照定义计算
mean_x = x.mean((0, 2, 3))  # 在 NHW上计算均值和方差
std_x = x.std((0, 2, 3), unbiased=False)
x_out_2 = (x - mean_x[None, :, None, None]) / std_x[None, :, None, None]

# x_out_1 应与 x_out_2 相等
"""
>>> x_out_1.view(3, 5, -1)
tensor([[[ 0.5701,  1.3119,  0.6911, -1.5281],
         [-0.2640,  0.6958, -0.4879,  2.6233],
         [ 1.5883,  1.3217, -0.9401, -0.8484],
         [ 0.6178,  0.7098,  0.6252, -0.1542],
         [-1.0076, -0.6226,  0.6902, -0.9112]],

        [[ 1.0838,  0.4721,  1.2620, -0.9831],
         [-0.0582,  0.7492, -0.1682, -0.8531],
         [ 0.2192, -0.9547, -0.8769, -1.0408],
         [-1.6932,  0.2731, -1.1455, -0.9619],
         [-0.3389, -0.1145, -0.2434, -1.3969]],

        [[-1.3717, -1.0275,  0.0167, -0.4972],
         [-0.1614, -0.5248,  0.0912, -1.6418],
         [ 1.6850, -0.3543, -0.3061,  0.5070],
         [-0.7309, -0.5870,  1.5495,  1.4972],
         [-0.5570,  1.7374,  1.4123,  1.3522]]])
>>> x_out_2.view(3, 5, -1)
tensor([[[ 0.5701,  1.3119,  0.6911, -1.5281],
         [-0.2640,  0.6958, -0.4879,  2.6233],
         [ 1.5883,  1.3217, -0.9401, -0.8484],
         [ 0.6178,  0.7098,  0.6252, -0.1542],
         [-1.0076, -0.6226,  0.6902, -0.9112]],

        [[ 1.0838,  0.4721,  1.2620, -0.9831],
         [-0.0582,  0.7492, -0.1682, -0.8531],
         [ 0.2192, -0.9547, -0.8769, -1.0408],
         [-1.6932,  0.2731, -1.1455, -0.9619],
         [-0.3389, -0.1145, -0.2434, -1.3969]],

        [[-1.3717, -1.0275,  0.0167, -0.4972],
         [-0.1614, -0.5248,  0.0912, -1.6418],
         [ 1.6850, -0.3543, -0.3061,  0.5070],
         [-0.7309, -0.5870,  1.5495,  1.4972],
         [-0.5570,  1.7374,  1.4123,  1.3522]]])
"""

2. LayerNorm

API: CLASS torch.nn.LayerNorm(normalized_shape, eps=1e-05, elementwise_affine=True, device=None, dtype=None)

\[y=\frac{x-\text{E}[x]}{\sqrt{\text{Var}[x] + \epsilon}} * \gamma + \beta\]

在CHW上计算均值与方差，示例代码如下：

  • 如果输入是 [N, C, H, W]形式，即API示例中的Image Example
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

N, C, H, W = 3, 5, 2, 2
x = torch.rand(N, C, H, W)

# nn.LayerNorm计算
ln_layer = torch.nn.LayerNorm([C, H, W], eps=0., elementwise_affine=False)
x_out_1 = ln_layer(x)  # [N, C, H, W]

# 按照定义计算
x_mean = x.mean([1, 2, 3])
x_std = x.std([1, 2, 3], unbiased=False)
x_out_2 = (x - x_mean[:, None, None, None]) / x_std[:, None, None, None]

# x_out_1 应与 x_out_2 相等
"""
>>> x_out_1.view(3, 5, -1)
tensor([[[ 0.6501,  1.5364,  0.7946, -1.8568],
         [-0.6528,  0.1166, -0.8324,  1.6618],
         [ 1.2697,  0.9812, -1.4672, -1.3680],
         [ 0.4042,  0.4850,  0.4107, -0.2747],
         [-0.8916, -0.5898,  0.4390, -0.8160]],

        [[ 2.0325,  1.1983,  2.2755, -0.7861],
         [ 0.0332,  0.7719, -0.0675, -0.6942],
         [ 0.3477, -1.1027, -1.0066, -1.2091],
         [-1.2681,  0.7054, -0.7184, -0.5341],
         [ 0.1706,  0.3713,  0.2560, -0.7758]],

        [[-1.5146, -1.0963,  0.1726, -0.4520],
         [-0.3965, -0.6928, -0.1905, -1.6036],
         [ 1.5817, -0.6635, -0.6105,  0.2847],
         [-0.6113, -0.4826,  1.4282,  1.3815],
         [-0.3637,  1.4651,  1.2060,  1.1581]]])
>>> x_out_2.view(3, 5, -1)
tensor([[[ 0.6501,  1.5364,  0.7946, -1.8568],
         [-0.6528,  0.1166, -0.8324,  1.6618],
         [ 1.2697,  0.9812, -1.4672, -1.3680],
         [ 0.4042,  0.4850,  0.4107, -0.2747],
         [-0.8916, -0.5898,  0.4390, -0.8160]],

        [[ 2.0325,  1.1983,  2.2755, -0.7861],
         [ 0.0332,  0.7719, -0.0675, -0.6942],
         [ 0.3477, -1.1027, -1.0066, -1.2091],
         [-1.2681,  0.7054, -0.7184, -0.5341],
         [ 0.1706,  0.3713,  0.2560, -0.7758]],

        [[-1.5146, -1.0963,  0.1726, -0.4520],
         [-0.3965, -0.6928, -0.1905, -1.6036],
         [ 1.5817, -0.6635, -0.6105,  0.2847],
         [-0.6113, -0.4826,  1.4282,  1.3815],
         [-0.3637,  1.4651,  1.2060,  1.1581]]])
"""
  • 如果输入是 [N, L, C]形式，即API示例中的NLP Example（图像描述中通常是这种数据组织形式），则均值和方差均在C上进行求取，即在输入数据的最后一维上求均值和方差
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

N, L, C = 3, 4, 5
x = torch.rand(N, L, C)

# nn.LayerNorm计算
ln_layer = torch.nn.LayerNorm(C, eps=0., elementwise_affine=False)
x_out_1 = ln_layer(x)  # [N, L, C]

# 按照定义计算
x_mean = x.mean(-1)
x_std = x.std(-1, unbiased=False)
x_out_2 = (x - x_mean[:, :, None]) / x_std[:, :, None]
"""
>>> x_out_1
tensor([[[-0.2380, -0.2267,  1.9469, -0.7811, -0.7011],
         [ 1.8029, -1.1073, -0.5569,  0.2497, -0.3884],
         [-1.1464, -0.3209,  1.6030,  0.6406, -0.7764],
         [-0.0740, -1.6507,  0.7076,  1.2997, -0.2825]],

        [[ 0.7822, -0.4960,  0.9142,  0.5369, -1.7373],
         [-1.7976, -0.0445,  0.3672,  1.2590,  0.2159],
         [ 0.7396,  1.1869, -1.1813, -1.2006,  0.4555],
         [ 1.0684,  1.0592, -1.0150,  0.1810, -1.2937]],

        [[-0.4093,  1.6552,  0.4399, -0.3537, -1.3320],
         [-0.8034,  0.9525,  1.3389, -1.2672, -0.2208],
         [ 0.2419, -1.4972, -0.6267,  0.4232,  1.4588],
         [-0.7910, -1.3169, -0.1005,  1.4134,  0.7951]]])
>>> x_out_2
tensor([[[-0.2380, -0.2267,  1.9469, -0.7811, -0.7011],
         [ 1.8029, -1.1073, -0.5569,  0.2497, -0.3884],
         [-1.1464, -0.3209,  1.6030,  0.6406, -0.7764],
         [-0.0740, -1.6507,  0.7076,  1.2997, -0.2825]],

        [[ 0.7822, -0.4960,  0.9142,  0.5369, -1.7373],
         [-1.7976, -0.0445,  0.3672,  1.2590,  0.2159],
         [ 0.7396,  1.1869, -1.1813, -1.2006,  0.4555],
         [ 1.0684,  1.0592, -1.0150,  0.1810, -1.2937]],

        [[-0.4093,  1.6552,  0.4399, -0.3537, -1.3320],
         [-0.8034,  0.9525,  1.3389, -1.2672, -0.2208],
         [ 0.2419, -1.4972, -0.6267,  0.4232,  1.4588],
         [-0.7910, -1.3169, -0.1005,  1.4134,  0.7951]]])
"""

3. InstanceNorm2d

API: CLASS torch.nn.InstanceNorm2d(num_features, eps=1e-05, momentum=0.1, affine=False, track_running_stats=False, device=None, dtype=None)

\[y=\frac{x-\text{E}[x]}{\sqrt{\text{Var}[x] + \epsilon}} * \gamma + \beta\]
  • 输入: [N, C, H, W]
  • 输出: [N, C, H, W] (与输入维度一致)

在HW上求均值和方差，代码示例如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

N, C, H, W = 3, 5, 2, 2
x = torch.rand(N, C, H, W)

# nn.InstanceNorm2d计算
in_layer = torch.nn.InstanceNorm2d(C, eps=0., affine=False, track_running_stats=False)
x_out_1 = in_layer(x)

# 根据定义计算
x_mean = x.mean((-1, -2))
x_std = x.std((-1, -2), unbiased=False)
x_out_2 = (x - x_mean[:, :, None, None]) / x_std[:, :, None, None]
"""
>>> x_out_1.view(3, 5, -1)
tensor([[[ 1.5311,  0.2455, -0.9808, -0.7958],
         [-0.9634, -0.1927, -0.5097,  1.6658],
         [ 0.6410,  1.2393, -1.3178, -0.5626],
         [ 1.2098, -1.1274,  0.7531, -0.8355],
         [-0.5653,  1.6005,  0.0223, -1.0575]],

        [[ 0.5257,  1.3195, -1.2969, -0.5484],
         [-0.7867, -1.1250,  1.3355,  0.5762],
         [ 1.0166,  0.2899, -1.6605,  0.3540],
         [ 0.3264,  1.4894, -0.7927, -1.0231],
         [ 1.3285,  0.4290, -0.3755, -1.3820]],

        [[-1.5102, -0.2778,  1.0419,  0.7461],
         [ 0.3678, -1.1810, -0.6277,  1.4408],
         [ 1.7132, -0.5482, -0.3753, -0.7897],
         [ 0.7189,  0.9644, -0.0879, -1.5954],
         [-0.2354, -0.9607,  1.6719, -0.4759]]])
>>> x_out_2.view(3, 5, -1)
tensor([[[ 1.5311,  0.2455, -0.9808, -0.7958],
         [-0.9634, -0.1927, -0.5097,  1.6658],
         [ 0.6410,  1.2393, -1.3178, -0.5626],
         [ 1.2098, -1.1274,  0.7531, -0.8355],
         [-0.5653,  1.6005,  0.0223, -1.0575]],

        [[ 0.5257,  1.3195, -1.2969, -0.5484],
         [-0.7867, -1.1250,  1.3355,  0.5762],
         [ 1.0166,  0.2899, -1.6605,  0.3540],
         [ 0.3264,  1.4894, -0.7927, -1.0231],
         [ 1.3285,  0.4290, -0.3755, -1.3820]],

        [[-1.5102, -0.2778,  1.0419,  0.7461],
         [ 0.3678, -1.1810, -0.6277,  1.4408],
         [ 1.7132, -0.5482, -0.3753, -0.7897],
         [ 0.7189,  0.9644, -0.0879, -1.5954],
         [-0.2354, -0.9607,  1.6719, -0.4759]]])
"""

4. GroupNorm

API: CLASS torch.nn.GroupNorm(num_groups, num_channels, eps=1e-05, affine=True, device=None, dtype=None)

\[y=\frac{x-\text{E}[x]}{\sqrt{\text{Var}[x] + \epsilon}} * \gamma + \beta\]
  • 输入: [N, C, *]
  • 输出: [N, C, *] (与输入维度一致)

令输入维度为[N, C, H, W]，首先对C进行分组， [N, C, H, W]–> [N, g, C//g, H, W]，然后在C//g,H,W（即后三个维度方向）上求均值和方差，示例代码如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58

N, C, H, W = 3, 6, 2, 2
x = torch.rand(N, C, H, W)  # [N, C, H, W]

# nn.GroupNorm求解
# 把 C=6，划分为 2 组
gn_layer = torch.nn.GroupNorm(num_groups=2, num_channels=C, eps=0., affine=False)
x_out_1 = gn_layer(x)

# 按照定义求解
x = x.view(N, 2, C // 2, H, W)  # [N, C, H, W] --> [N, g, C//g, H, W]
x_mean = x.mean((2, 3, 4))
x_std = x.std((2, 3, 4), unbiased=False)
x_out_2 = (x - x_mean[:, :, None, None, None]) / x_std[:, :, None, None, None]
x_out_2 = x_out_2.view(N, C, H, W)
"""
>>> x_out_1.view(3, 6, -1)
tensor([[[-0.1290, -1.5416,  1.3508,  0.0259],
         [ 0.8220, -1.1861, -0.8968,  0.5246],
         [-1.1964, -0.2531,  1.0820,  1.3977],
         [ 0.6300, -1.5861, -1.6701, -0.3855],
         [ 0.6316,  1.1035, -0.2076,  0.7945],
         [ 0.9343,  0.2422, -1.4284,  0.9415]],

        [[-1.4208, -0.4870,  0.4255, -0.7972],
         [ 1.8013,  0.3366,  1.8382, -0.7250],
         [ 0.5121, -0.9930,  0.1396, -0.6302],
         [ 0.2940,  0.9422,  0.2082, -0.0493],
         [ 1.6209, -0.2877, -1.0879,  0.6238],
         [-0.5238, -1.7207,  1.3058, -1.3255]],

        [[ 0.1376, -1.6736,  1.5494, -0.6100],
         [-0.3534,  0.5688, -0.2642,  0.5488],
         [-0.8490,  1.9884, -0.0916, -0.9512],
         [-0.6563,  1.4381,  1.5124,  1.1264],
         [-0.9688, -0.5808,  0.1888,  0.0883],
         [-1.2760, -0.8207,  1.0518, -1.1034]]])
>>> x_out_2.view(3, 6, -1)
tensor([[[-0.1290, -1.5416,  1.3508,  0.0259],
         [ 0.8220, -1.1861, -0.8968,  0.5246],
         [-1.1964, -0.2531,  1.0820,  1.3977],
         [ 0.6300, -1.5861, -1.6701, -0.3855],
         [ 0.6316,  1.1035, -0.2076,  0.7945],
         [ 0.9343,  0.2422, -1.4284,  0.9415]],

        [[-1.4208, -0.4870,  0.4255, -0.7972],
         [ 1.8013,  0.3366,  1.8382, -0.7250],
         [ 0.5121, -0.9930,  0.1396, -0.6302],
         [ 0.2940,  0.9422,  0.2082, -0.0493],
         [ 1.6209, -0.2877, -1.0879,  0.6238],
         [-0.5238, -1.7207,  1.3058, -1.3255]],

        [[ 0.1376, -1.6736,  1.5494, -0.6100],
         [-0.3534,  0.5688, -0.2642,  0.5488],
         [-0.8490,  1.9884, -0.0916, -0.9512],
         [-0.6563,  1.4381,  1.5124,  1.1264],
         [-0.9688, -0.5808,  0.1888,  0.0883],
         [-1.2760, -0.8207,  1.0518, -1.1034]]])
"""
Blogs, DeepLearning
Normalization BasicKnow
This post is licensed under CC BY 4.0 by the author.
Recently Updated
Contents

LeetCode97-交错字符串

秋招记录-胡言乱语